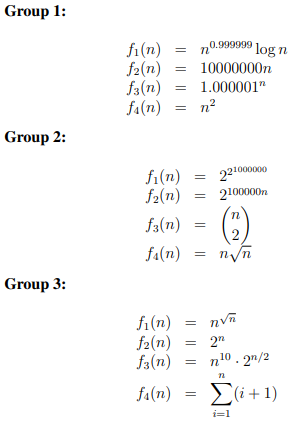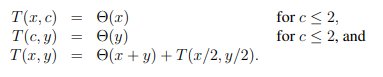1차원 peak 값
-
가장 간단한 알고리즘 : 왼쪽에서 부터 시작, 최악의 경우 n을 모두 다 봐야하는 세타(n) 복잡도
-
개선된 알고리즘 : 이진 탐색 알고리즘, T(n) = T(n/2) + 세타(1), T(n) = 세타(1) * log2n
2차원 peak 값
- 최악의 경우 n=m, m=n 세타(n^2) 복잡도
- 중앙 열 j = m/2을 선택한다.
- (i, j)에서 j열의 최댓값을 찾는다.
- (i, j − 1), (i, j), (i, j + 1)를 비교한다.
- (i, j − 1) > (i, j)이면 왼쪽 열을 선택한다.
- 오른쪽도 똑같이 진행한다.
- 두 조건 모두 만족하지 않으면, (i, j)가 2차원 극댓값이다 ← 왜일까?
- 열 개수가 절반으로 줄어든 새로운 문제를 푼다.
- 열이 1개 남으면, 최댓값을 찾고 끝난다.
T(n,m) = T(n,m/2) + 세타(n) // n*m 행렬에서 global max값을 찾는것은 n번해야함
T(n,1) = 세타(n) T(n,m) = 세타(n)*nlog2m
Problem Set
Problem 1-1. Asymptotic Practice
big-O 빠른 순서 대로 정렬
[Group1]
f1(n), f2(n), f4(n), f3(n)
- f1(n) = O(n^0.999999·n^0.000001) = O(n) = O(f2(n))
- 선형 f2(n) = O(f4(n))
- f4(n) = O(f3(n))
- 2차 함수
[Group2]
f1(n), f4(n), f3(n), f2(n)
- 지수 곱에도 불구하고 f1(n)은 상수 f4(n) 보다 작음
- f4(n)는 n^1.5 f3(n)은 n(n-1)/2 -> Θ(n^2)
- f3(n) O(f2(n))
[Group3]
f4(n), f1(n), f3(n), f2(n)
- f4(n) = n((n+1)+2)/2 = n(n+3)/2 = Θ(n^2)
- f1(n) = (2^logn)^√n = 2^√n-logn
- f3(n) = n2^log(n^10)*2^n/2 = 2^n/2+10logn
Problem 1-2. Recurrence Relation Resolution
계산 복잡도 구하는 문제
1. T(x,y) = c(x+y) + T(x/2,y/2)
T(x,y) = c(x+y) + c((x+y)/2) + c((x+y)/4) + c((x+y)/8) + …
2c(x+y) -> c(x+y) -> Θ(x+y) -> Θ(n)
2. T(x,y) = Θ(x) + Θ(y/2) + T(x/2,y/2)
T(x,y) = Θ(x+y) + T(x/2,y/2)
출처