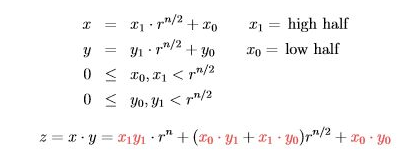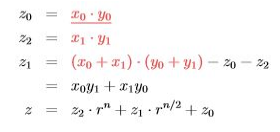무리수 : 피타고라스는 정사각형의 대각선의 길이와 한 변의 길이의 비율은 정수비로 표현할 수 없다는 것을 발견했다.
카탈란수 : 올바른 괄호 구조 문자열로 이루어진 집합 P는 아래와 같이 귀납적으로 정의한다.
- λ ∈ P (λ 는 빈 문자열)
- 만약 α, β ∈ P이면, (α)β ∈ P이다.
빈 문자열이 아닌 모든 올바른 괄호 구조 문자열은 특정한 α, β쌍을 이용하여 규칙 2로부터 얻을 수 있다.
Cn : n쌍의 괄호를 가지는 올바른 괄호 구조 문자열의 개수 C0 빈 문자열
Cn+1 : 특정한 규칙 2로부터 얻어지는 n+1쌍의 괄호를 가지는 올바른 괄호
k쌍의 괄호를 가진 문자열은 알파로부터 얻어지고, n-k쌍의 괄호를 가진 문자열은 베타로 부터 얻어진다.
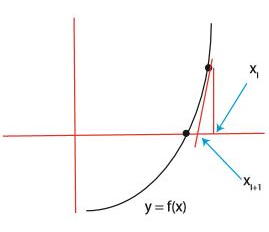
뉴튼 방법
연속 근사법을 이용하여 f(x)=0의 해를 찾는 방법 f(x)=x^2 - a
점(xi,f(x<sub</sub>))에서의 접선은 y = f(xi)+f’(xi)*(x-xi)이고 f’(xi)는 도함수이다. xi+1은 x축과의 교점이 된다.
제곱근
f(x) = x^2 - a
xi+1 = xi - (xi^2-a)/2xi = xi + (a/xi)/2
고정밀도 계산
루트2의 d자릿수 계산 : 1.41414213562373…
정수가 필요하기 때문에, 무리수의 정수 \(10<sup>d</sup>\sqrt{2} = \sqrt{2*10<sup>2d</sup>}\) 부분만을 이용
고정밀도 곱셈
두개의 n자릿수 숫자를 곱하는 경우 필요하다.
절반 크기를 가지는 숫자들을 4번 곱셈으로 계산 -> Θ(n^2), 제곱 시간 알고리즘이 된다
카라추바 알고리즘
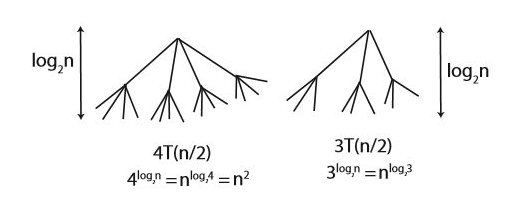
위와 같이 곱셈을 표현하면, 위의 계산에서 총 3번의 곱셈을 수행한다.
<img src=”../../../assets/images/karatsuba_alogrithm_3.PNG” alt=”karatsuba_alogrithm”3 />
따라서 이 방법은 Θ(n^2)보다 짧은 시간에 가능하다.
출처