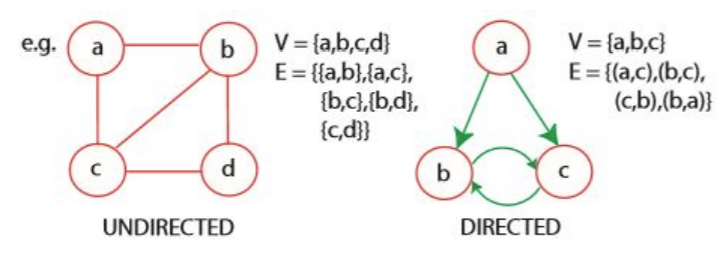
그래프 G = (V,E)
- V = 정점의 집합(임의의 레이블)
- E = 간선의 집합 i.e. 정점의 쌍(v,w)
- 순서쌍 => 그래프의 방향이 있는 간선
- 비순서쌍 => 무방향
그래프 탐색 예시
- 시작 점 s에서 원하는 정점으로의 경로를 찾는다.
- 그래프의 또는 s에서 도달할 수 있는 모든 정점과 간선을 방문한다.
응용 사례
- 웹 크롤링(구글이 페이지를 찾는 방법)
- 소셜 네트워킹(페이스북이 친구 찾기를 사용하는 법)
- 네트워크 브로드캐스트 라우팅
- 가비지 컬렉션
- 모델 검사(무한 상태 기계)
- 수학적 추측 확인하기
- 퍼즐이나 게임 풀기
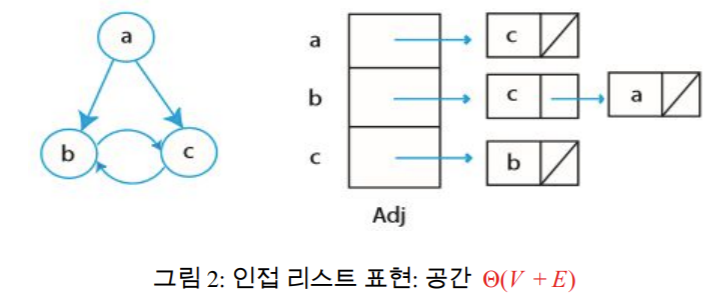
그래프 표현: 자료구조
|V| 연결 리스트의 배열 Adj - 각 정점 u ∈ V에 대해, Adj[u]는 u의 이웃들을 저장한다.
예: {v ∈ V |(u,v) ∈ E}
방향 그래프에서 (u,v)는 나가는 간선이다.
- 파이썬 : Adj = 리스트 / 집합 값의 딕셔너리 : 정점 = 해시 가능한 것 (예: int, tuple)
- 장점 : 같은 정점에 여러 그래프가 있을 수 있음
객체 지향 변형
- 각 정점 u에 대한 객체
- u.neighbors = 이웃한 점들의 리스트 (예:Adj[u])
입력목록:
- 간선도 객체로 만들 수 있다.
- u.edges = u에서 나가는 간선의 리스트
- 장점 : 해싱 없이도 간선을 저장할 수 있다.
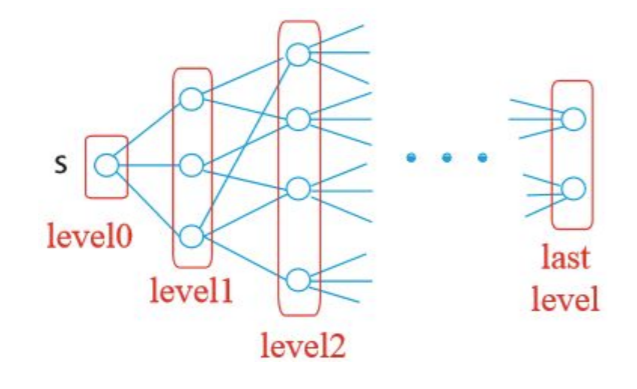
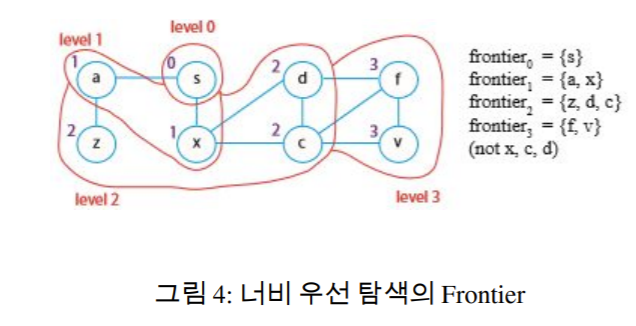
너비 우선 탐색(BFS)
s에서 레벨별로 그래프를 탐색한다
- level0 = {s}
- level i = 최소 i개의 간선의 경로로 도달할 수 있는 정점
- 모든 나가는 간선을 사용해 level i-1에서 level i > 0을 만든다. 하지만 이전 level의 정점은 무시한다.
BFS algorithm (Breadth-Fisrt Search)
BFS(V, Adj,s):
level = {s:0}
parent = {s: None}
i = 1
froties = [s]
while fronties:
next = {}
for u in frontier:
for v in Adj[u]:
if v not in level:
level[v] = i
parent[v] = u
next.append(v)
frontier = next
i += 1
분석
- 정점 v가 next를 (다음으로는 fronties를) 한 번만 방문한다. (level[v] 가 정의되므로) 기본 경우 : v = s
- => Adj[v]는 루프를 한 번만 통과한다.
- O(E) 시간
- O(V+E) (“선형 시간”) v에서 도달할 수 없는 정점을 리스트한다. (level이 지정되지 않은 정점)
최단 경로:
- 각 정점 v에 대해, s에서 v로 갈 수 있는 가장 적은 수의 간선은
level[u] if u assigned level
else (no path)
- 부모 포인터는 최단 경로 트리를 형성한다. 각 v에 대한 최단 경로의 조합 => 최단 경로를 찾으려면 v를 찾고, parent[v]를 찾고, parent[parent[v]]를 찾아 s에 도달하거나 끝날 때까지 찾는다.
출처