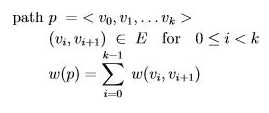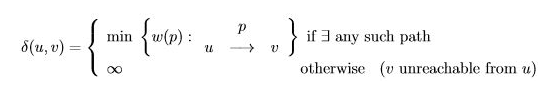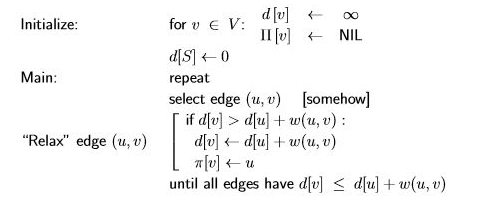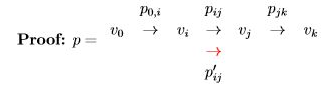공식화: 가중 그래프 G(V,E) W : E -> R의 문제

두 알고리즘 : 다익스라 O(VlogV+E)는 음이 아닌 가중치를 가정, 벨만-포드 O(V E)는 일반적인 알고리즘

가중 그래프 G(V,E), W : E -> R의 모델

• V = 정점(도로의 교차점)
• E = 간선(거리, 도로); 방향 간선 (일반통행 도로)
• W(U,V) = 간선 (u,v)의 가중치 (거리, 통행료)

p는 V₀에서 V_k까지의 경로 p를 의미한다. (V₀)는 V₀에서 V₀까지의 가중치 0인 경로를 의미한다.

u에서 v까지 최단 경로의 가중치를 다음과 같이 정의한다.

단일 출발 최단 경로 :

G(V,E), w와 시작 정점 S가 주어져 있을 때, S부터 각각의 v ∈ V 까지의 δ(S, V )[와 최단 경로]를 찾아라.

자료구조

d[v]는 v로 가는 더 좋은 경로를 찾을 때 마다 줄어든다.

음의 가중치 간선

• 몇몇 적용에는 자연스럽다.(예, 가중치로 로그가 쓰이는 경우)
• 몇몇 알고리즘은 음의 가중치를 갖는 간선을 허용하지 않는다. (예, 다익스트라)
• 음의 가중치를 갖는 간선이 있으면, 음의 사이클이 있을 수 도 있다. -> 최단 경로가 없을 수 도 있다.

음의 간선이 있는 경우, 최단 경로 알고리즘은 음의 사이클을 찾을 수 있어야 한다.(예, 벨만-포드)

최단 경로 알고리즘의 일반적인 구조 (음의 사이클이 없는 경우)

n개의 간선이 있고 첫 세 개의 간선이 2^n/2의 가중치를 갖고, 두 번째 간선들은 2^(n/2)-1의 가중치를 갖는 식으로 된다. 경로적으로 간선을 선택하면 d(v_n-1)의 첫 값이 (2^n/2+2^(n/2)-1+…+4+2+1)이 될 것이다. 이 순서로, V_n-3과 V_n-1을 연결하는 가중치가 1인 간선을 완화할 수 있을 것이다. 그러면, d(V_n-1)는 1이 줄어들 것이다. 그리고 V_n-5와 V_n-3을 연결하는 가중치 2인 간선에 대해 완화하면, d(V_n-2)가 2만큼 줄어들 것이다. 그 후로, d(V_n-1)을 1만큼 줄이기 위해 간선 (d(V_n-3),d(V_n-2))와 (V_n-2, V_n-1)에 대해 완화할 수 있다. 그리고 또, 간선 (V_n-3,V_n-1)에 대해 완화한다. 이런 식으로 d(V_n-1)를 한 번 완화할 때마다 1씩 줄이면서 (2^n/2+2^(n/2)-1+…+4+2+1)까지 줄일 수 있을 것이다. 이는 O(2^n/2) 시간이 걸린다.

최적 부분 구조

정리 : 최단 경로의 부분 경로는 최단 경로이다.

p =< v0 , v1 , …, vk > 를 최단 경로라고 하고

pij =< v0 , vi+1 , …, vj > 0 ≤ i ≤ j ≤ k 라고 하면

pij는 최단 경로이다.

만약 pij’가 pij보다 작다고 하면, pij대신 pij’를 사용하게 되면 p보다 작아진다.

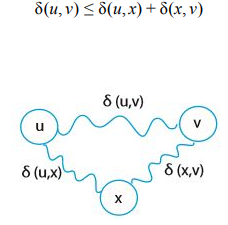
삼각부등식

정리 : 모든 u,v,x ∈ X 에 대해

출처

MIT 파이썬을 이용한 알고리즘