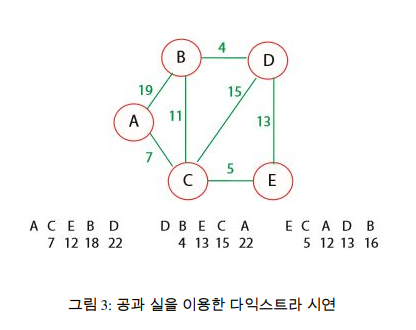
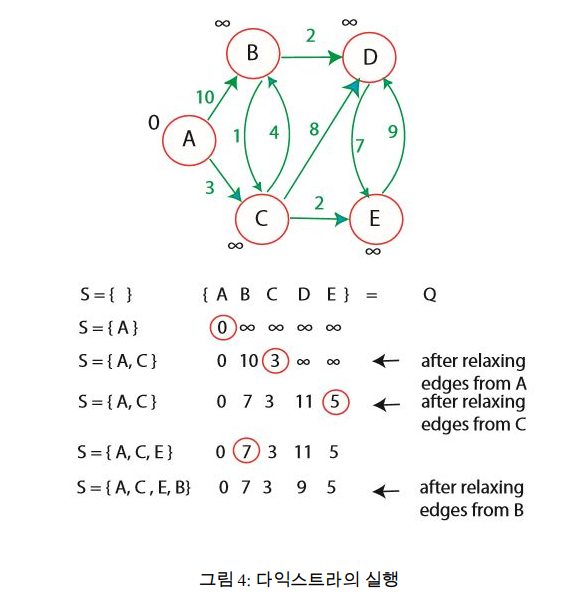
각 간선 (u, v) ∈ E 에 대하여, w(u, v) ≥ 0 을 가정하고, 정점의 집합 S 에 최단 경로의 값이 결정된 정점만을 유지한다. 최소인 최단 경로 어림을 가지는 u 를 V − S 집합에서 반복적으로 선택하여, u 를 S 에 넣고, u 로부터 나가는 모든 간선에 대해 완화한다.
의사코드

전략: 다익스트라는 탐욕 알고리즘이다. V − S 에서 가장 가까운 정점을 선택하여 집합 S 에 넣는다.
타당성: 완화가 안전하다는 것은 안다. 중요 관찰점은 집합 S 에 정점 u 가 추가될 때마다 d[u] = δ(s, u) 가 된다는 것이다.
다익스트라의 복잡도
Θ(V) 번의 우선순위 큐 삽입 연산
Θ(V) 번의 EXTRACT-MIN 연산
Θ(E) 번의 DECREASE-KEY 연산
배열을 이용한 구현:
Θ(V) : 최소의 원소 추출
Θ(1) : 키 감소 연산
계: Θ(V · V + E · 1) = Θ(V^2+E)= Θ(V^2)
이진 최소 힙을 이용한 구현:
Θ(lgV ) : 최소의 원소 추출
Θ(lgV ) : 키 감소 연산
계: Θ(VlgV + ElgV)
피보나치 힙:
Θ(lgV) : 최소의 원소 추출
Θ(1) : 키 감소 연산
분할상환 비용
계: Θ(V lgV + E)
출처