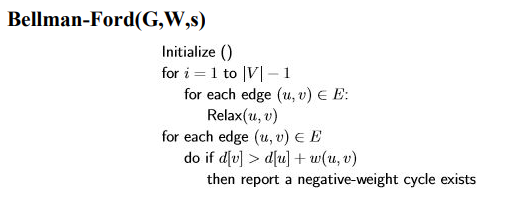음의 순환이 없다면 알고리즘의 마지막엔 d[v]=δ(s,v) 이다.
그래프 G = (V,E)가 음의 순환을 가지고 있지 않으면 벨만 포드 알고리즘의 종료 후 모든 그래프의 정점 v ∈ V에 대해 d[v] = δ(s,v) 이다.
증명
v ∈ V를 그래프 내 임의의 정점이라고 둔다. 정점 v0 = s에서 vk = v 까지의 경로 p = < v0 , v1 ,…, vk > 를 최소 개수의 간선을 가진 최단 경로라고 둔다.음의 순환이 없으면 경로 p는 단순 경로이다.
알고리즘의 시작에서 d[v0] = 0 = δ(s, v0) 이고 음의 순환이 없으므로 이 값은 변하지 않는다.
모든 간선 E에대해 첫 번째 완화 과정을 거치면, d[v1]의 값은 다음과 같이 갱신된다. d[v1] = δ(s,v1). 첫 번째 계산을 통해 간선 (v0,v1)이 완화되고 이 최단 경로보다 더 짧은 경로를 찾을 수 없기 때문이다.
간선 E에 대해 두 번째 완화 과정을 거치면, d[v2] = δ(s,v2)이다. 두 번째 완화 과정에서 간선 (v1,v2)가 완화되기 때문이다.
모든 간선 E에 대해 i번 완화 가정을 가지면, d[vi] = δ(s,vi)로 값이 갱신된다.
| k <= | V | -1 번째 완화 과정을 E의 각 간선에 대해 실행하면, d[vk]=d[v]=δ(s,v)의 결과를 얻을 수 있다. |
따름 정리
| V | -1의 완화 과정 이후에도 d[v]의 값이 수렴하지 않으면 s로 부터 도달할 수 있는 음의 순환이 존재한다. |
증명
|V|-1의 완화 과정을 거친 후에도 완호될 수 있는 간선을 찾을 수 있다면 현 최단 경로가 단순 경로가 아니고 같은 정점을 중복 방문한다는는 것을 의미한다. 순환을 포함한 이 경로가 단순 경로보다 가중치가 작으므로 이 순환은 음의 가중치를 가진다.
최장 단순 경로와 최단 단순 경로
양의 가중치를 가지는 그래프에서 최장 단순 경로를 찾는 문제는 NP-hard 문제이다. 즉, 알려진 다항시간 알고리즘이 존재하지 않는다. 각 간선의 가중치를 음수화하고 벨만-포드 알고리즘을 이용해 최단 경로를 계산한다고 생각해보자. 벨만 포드 알고리즘은 음의 순환이 시작점에서 도달 가능하면 바로 종료해버리기 때문에 실질적으로 기존 그래프의 최장 경로를 계산하지 못한다.
NP-난해, NP-hard는 NP에 속하는 모든 판정 문제를 다항 시간에 다대일 환산할 수 있는 문제들의 집합이다. 다시 말하면, NP-난해는 적어도 모든 NP 문제만큼은 어려운 문제들의 집합이다. -위키백과-
유사하게 음의 순환을 가지고 있는 그래프가 있고, 정점 s에서 v까지의 최장 단순 경로를 계산하고 싶다면 벨만-포드 알고리즘을 사용할 수 없다. 최단 단순 경로를 구하는 문제 역시 NP-hard 이다.
출처