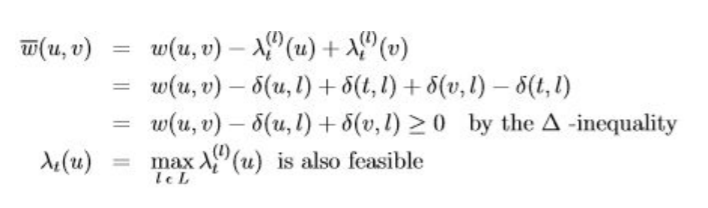양방향 탐색
알고리즘은 어떤 정점 w가 계산 되었을 때 끝난다. 즉 전진 탐색과 후진 탐색 모두의 우선순위 큐 Qf 와 Qb 에서 제거되었을 때 종료한다. 탐색이 종료하고 df(x) + db(x)의 값이 최소인 정점 x를 찾는다. 왼쪽의 예시에서처럼 x가 정점 w가 아닐 수도 있다.
Πf를 이용해서 s에서 x까지의 최단 경로를 찾고 Πb를 이용해서 t에서 x까지의 최단 경로를 거꾸로 찾는다. 이때 x는 Qf와 Qb모두에서 제거되었다.
목적지향 또는 A*
정점에 대해 잠재력 함수에 따라 간선의 가중치를 수정한다.
w (u, v) = w(u, v) − λ(u) + λ(v)
정확성
w (p) = w(p) − λt(s) + λt(t)
가중치 w 로 수정된 그래프에서도 최단 경로가 유지된다. 다익스트라를 적용하기 위해서 모든 간선 (u, v)에 대해서 w (u, v) ≥ 0 를 만족해야한다. 적절하고 조건을 만족하는 잠재력 함수를 찾아야한다.
랜드마크
그래프의 정점의 부분집합 랜드마크 집합 LCV가 있다. 모든 정점 u ∈ V, l ∈ L에 대해 δ(u, l)를 미리 계산한다. 각 랜드마크 l에 대한 잠재력 함수 λ (u) = δ(u, l) − δ(t, l) 이다.
사용가능성
출처