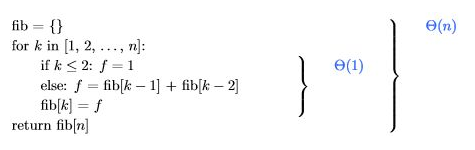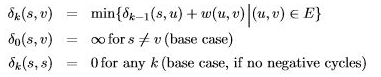동적 프로그래밍 (DP)

• 강력한 알고리즘 디자인 기법
• 보기에는 지수 시간이 걸리는 많은 문제도 DP를 사용하면 다항 시간에 풀 수 있음
• 특히 최적화 문제 (최소화/최대화)에 쓰임(최단 경로 문제)

피보나치 수

F₁=F₂=1; F_n=F_n-1+F_n-2

단순 알고리즘

• 모든 k에 대해 fib(k)는 처음 호출될 때만 재귀 호출을 한다.
• n개의 메모이제이션 되지 않은 호출만이 존재한다.
• 메모이제이션 된 호출은 거의 꽁짜다 Θ(1) time
• 재귀를 무시한다면 호출당 Θ(1) 시간이 걸린다.

상향식 DP 알고리즘

• 메모이제이션 DP와 계산이 정확히 일치한다.

• 일반적으로 하위 문제 종속 방향성 비순환 그래프의 위상 정렬

• 재귀가 없기 때문에 사실상 더 빠르다
• 분석이 더 쉽다
• 공간을 아낄 수 있다. 최근 두 피보나치 수만 기억한다.

최단 경로

• 재귀 공식 :δ (s, v) = min{w(u, v) + δ(s, u) (u, v) ∈ E}
• 메모이제이션 DP 알고리즘: 순환이 있다면 무한 시간이 걸림
• 방향성 비순환 그래프에서는 O(V+E) 시간에 실행

하위 문제 종속은 비순환이어야 함

• 하위 문제가 늘어난다면 순환 종속을 없앨 수 있다. δk(s, v) = k개 이하 간선을 사용한 s에서 v까지의 최단 경로

• 재귀

• 목표 : δ(s, v) = δ

  V

  −1(s, v) (음수 순환이 없는 경우)

• 메모이제이션
• time : #subprolbems*time/subproblem
• 실제로는 δk(s, v)에 대해 Θ(진입차수(v))

재귀 디자인 방법 -s에서 v까지의 최단 거리 계산

• 경로에서 마지막 간선 알 수 없음
• (u,v)라고 추측
• path is shortest s -> u path + edge(u,v)
• cost is delta_k-1(s,u) + w(u,v)

• 최선의 추측을 찾기 위해 모든 (

  V

  )값들을 시도해보고 최적을 찾는다.

• 비결 : 하위 문제당 적은 (다항) 가능한 추측 - 하위 문제당 시간을 결정하는 요인이다.
• DP = 재귀 + 메모이제이션 + 추측

출처

MIT 파이썬을 이용한 알고리즘